

Auteur : Lascap Ertîamel
4. La gravitation et l'expansion
Le principe du modèle CP est, semble t-il, compatible avec la relativité générale.
Le principe est celui du repos local. C'est-à-dire que dans son propre repère, un observateur ne doit observer aucune différence s'il est au repos ou s'il est dans un champ de déformation gravitationnel extérieur à son propre repère.
Le principe de repos local vient à considérer le repère comme immobile si aucune référence n'est faite à un autre repère. Sans référence à un repère extérieur, un observateur ne pourrait pas deviner si son propre repère est influencé par une déformation gravitationnelle (sauf à grande échelle avec les effets de marées). Par contre du point de vue extérieur, le repère se déplacerait en suivant la géodésique (plus court chemin entre deux points d'un espace courbe) issue de la déformation gravitationnelle.
La déformation de l'espace-temps à
proximité d'une masse (énergie 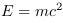 )
proviendrait directement de la création de CP due
à l'accroissement local d'énergie. Cette
création 'creuserait' (inclinerait) la trame de
l'Univers. Cette déformation étant ce que l'on
nome la déformation gravitationnelle ou le puit de
gravité.
)
proviendrait directement de la création de CP due
à l'accroissement local d'énergie. Cette
création 'creuserait' (inclinerait) la trame de
l'Univers. Cette déformation étant ce que l'on
nome la déformation gravitationnelle ou le puit de
gravité.
Du point de vue de l'observateur extérieur à cette déformation, le phénomène pourrait être perçu comme une 'densification' de cette zone de l'Univers.
Cette 'densification' amènerait un accroissement des distances pour tout objet observé au travers du puit de gravitation ou depuis celui-ci.
Le régime énergétique des CP, qui pose l'hypothèse d'une harmonisation de l'énergie entre CP, provoquerait le 'drainage' de l'énergie des CP externes à la zone de densité vers les CP à l'intérieur de la zone. L'effet serait une augmentation de la densité de la zone et une diminution de celle de l'extérieur. Ce qui amènerait un effet de répulsion de l'extérieur vers l'intérieur. Ce qui viendrait influencer la dynamique des galaxies. Pour les vieilles Galaxies, ce serait une des explications de leur dynamique influencée par la matière noire.
Cette harmonisation dépendrait de la conductance
d'énergie des CP (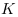 ). Plus
). Plus 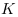 serait proche de zéro est plus
l'harmonisation serait lente. Dans ce cas, les jeunes Galaxies
ne subiraient pas les phénomènes liés
à la matière noire. Le drainage de
l'énergie externe au puits de gravitation n'étant
pas encore en place. Ce qui permettrait d'expliquer les
observations réalisées sur les Galaxies à
fort redshift (Galaxies très éloignées et
très jeunes).
serait proche de zéro est plus
l'harmonisation serait lente. Dans ce cas, les jeunes Galaxies
ne subiraient pas les phénomènes liés
à la matière noire. Le drainage de
l'énergie externe au puits de gravitation n'étant
pas encore en place. Ce qui permettrait d'expliquer les
observations réalisées sur les Galaxies à
fort redshift (Galaxies très éloignées et
très jeunes).
4.1 Corrélation entre le système
de mesures standard et le système de mesures CP

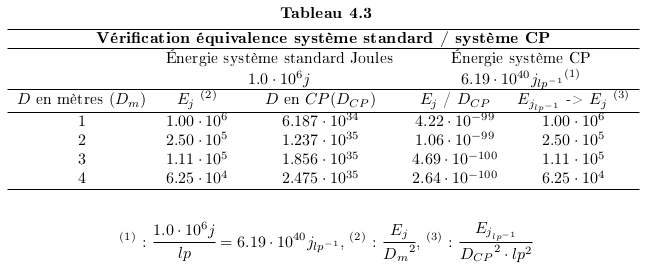
Dans l'Univers CP, la trame de l'Univers serait discontinue. La diminution des signaux émis suit les diminutions constatées dans notre système métrique. Pour rappel, le système de mesure du modèle CP est la Cellule de Planck (brique d'Univers). La diminution de l'intensité d'un signal lumineux, doit suivre les mêmes lois que celles constatées dans la réalité (cf. Figure 4.1).
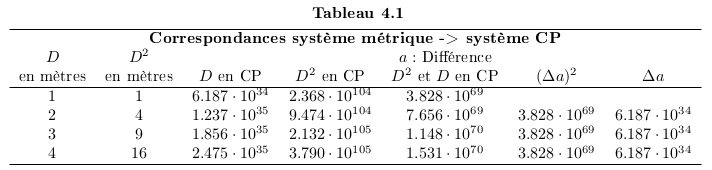
Ce qui nous donne la loi de variation suivante :

Le système CP n'est rien d'autre qu'un système de mesure différent de celui du système classique. La conversion est assurée de l'un à l'autre.
Pour garantir la conversion complète entre les deux systèmes de mesures, il faut vérifier la cohérence avec la diminution de l'énergie selon la distance dans les deux systèmes de mesures.
Dans le système classique, la mesure se fait en joules.
Les joules mesurent un effort en 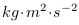 . En changeant le système de mesures
en CP sur la distance, l'unité de mesure devient le
nombre de transitions (
. En changeant le système de mesures
en CP sur la distance, l'unité de mesure devient le
nombre de transitions (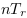 ). La conversion dans le système
standard se faisant par
). La conversion dans le système
standard se faisant par 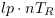 ,
, 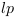 = longueur de Planck. Il
faut garantir que l'expression de l'énergie dans le
système de mesures compatible
= longueur de Planck. Il
faut garantir que l'expression de l'énergie dans le
système de mesures compatible 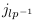 donne
les mêmes résultats dans le système standard
après conversion.
donne
les mêmes résultats dans le système standard
après conversion.
 Il y a bien correspondance entre le
système CP et le système standard. L'un peut
être utilisé en lieu et place de l'autre. Il faut
être attentif aux unités des systèmes de
mesures dans les calculs.
Il y a bien correspondance entre le
système CP et le système standard. L'un peut
être utilisé en lieu et place de l'autre. Il faut
être attentif aux unités des systèmes de
mesures dans les calculs.
Il n'est pas possible d'aborder la gravitation sans traiter la
constante 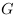 .
Cette constante est utilisé dans le modèle
Newtonien ainsi que dans la relativité
générale.
.
Cette constante est utilisé dans le modèle
Newtonien ainsi que dans la relativité
générale. 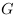 est exprimée dans le
modèle standard, il faut la convertire dans le
modèle CP :
est exprimée dans le
modèle standard, il faut la convertire dans le
modèle CP : 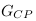 (cf. EC.
10 en annexes).
(cf. EC.
10 en annexes).
-
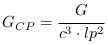 ;
; 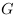 =
Constante de gravitation dans le système standard ;
=
Constante de gravitation dans le système standard ;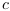 =
Vitesse de la lumière dans le système standard ;
=
Vitesse de la lumière dans le système standard ;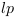 =
Longueur de Planck dans le système standard.
=
Longueur de Planck dans le système standard.
4.2 Principe de la déformation gravitationnelle
Etat de repos local
Comme pour la relativité générale, les CP
s'appuient sur le principe d'équivalence. Si nous posons
le postulat selon lequel un repère  qui subit une
accélération dans un repère
qui subit une
accélération dans un repère  , alors toute mesure
de dans
, alors toute mesure
de dans  ne doit pas permettre de détecter
l'accélération par rapport à
ne doit pas permettre de détecter
l'accélération par rapport à  . Nous appellerons cette
situation l'état de repos de
. Nous appellerons cette
situation l'état de repos de  . Si
. Si  "résistait"
à l'accélération, il ne serait plus au
repos. De l'énergie serait "dépensée" par
"résistait"
à l'accélération, il ne serait plus au
repos. De l'énergie serait "dépensée" par  et les objets tomberaient dans
et les objets tomberaient dans  .
.
Le meilleur moyen de vérifier l'état de  est de réaliser
une mesure de redshift
est de réaliser
une mesure de redshift 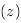 1
dans
1
dans  d'un signal émis dans
d'un signal émis dans  .
.
En réalisant des mesures (observations de  ) depuis
) depuis  , nous pouvons
établir la carte de la géométrie spatiale
de la zone (perçue depuis
, nous pouvons
établir la carte de la géométrie spatiale
de la zone (perçue depuis  ). Ces mêmes observations
faites depuis un autre repère aboutiraient à une
géométrie perçue différemment. En
relativité, tout n'est que comparaison entre
référentiels.
). Ces mêmes observations
faites depuis un autre repère aboutiraient à une
géométrie perçue différemment. En
relativité, tout n'est que comparaison entre
référentiels.
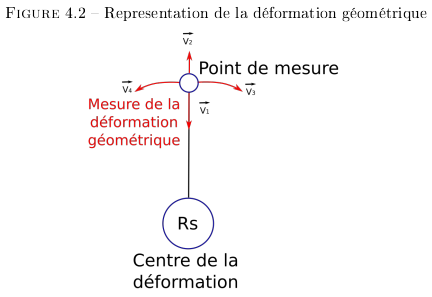
La Figure 4.2 montre la déformation de la
géométrie de l'espace au point de mesure CP.
L'état de repos de ce point fait en sorte que les mesures
effectuées (dans le référentiel de ce
point) ne constatent aucune déformation. C'est à
dire que les vecteurs 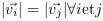 .
.
1 : 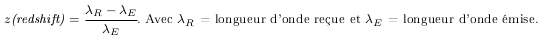
Forces de marées gravitationnelles
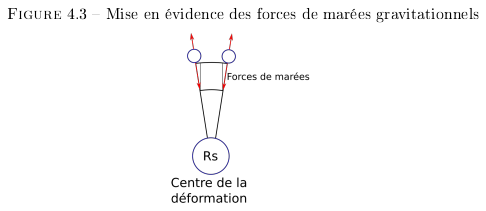
Le seul moyen de distinguer une accélération de nature gravitationnelle d'une non gravitationnelle, c'est de réaliser des meusures en deux points proches mais différents. Les vecteurs de la déformations spatiale ne seront pas parallèles. Ils convergeront vers le centre de la déformation gravitationnelle. Et à l'opposé, ils divergeront. Ce procédé permet également de déterminer les forces de marées gravitationnelles aux points de mesures.
Ces forces amènent des accélérations locales perpendiculaires à la direction vers le centre de la déformation comme le montre la Figure 4.3.
Agencement de la trame d'Univers
La gravitation sculpte l'agencement des CP entres elles. Les CP s'organisent autour de la déformation. Ajouté à l'état de repos local, cet agencement défini le parcours qu'aurait un objet, un photon, une particule qui ne subirait aucun effort externe. Cette approche est équivalente à celle de la RG (Relativité Générale). Les deux approches s'appuient sur le principe de moindre action. Dans les deux approches, les trajectoires sont rectilignes au sein d'un espace courbe.La courbure dans le système CP étant l'intégration des différents états de repos locaux des CP.
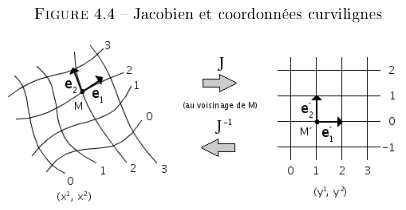
L'agencement et l'état de repos permettent de
définir une matrice Jaconienne2
(cf. Figure 4.4) de laquelle, par sa transposée il est
possible d'obtenir le tenseur métrique de la
relativité générale 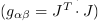 . Tenseur
métrique qui permet de déterminer les
géodésiques de l'espace sur lequel il est
défini.
. Tenseur
métrique qui permet de déterminer les
géodésiques de l'espace sur lequel il est
défini.
Plus simplement dans le système CP, la courbure
paramétrée 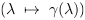 se détermine directement par
l'agencement et les états de repos locaux des CP dans
l'environnement de la déformation. La
géodésique se déterminant par les
transitions vers la CP la plus proche pour laquelle la
différence avec l'état de repos est minimale.
se détermine directement par
l'agencement et les états de repos locaux des CP dans
l'environnement de la déformation. La
géodésique se déterminant par les
transitions vers la CP la plus proche pour laquelle la
différence avec l'état de repos est minimale.
2 : Une matrice jacobienne est une matrice des dérivées partielles de premier ordre d'une fonction vectorielle.
Exemple :
- F une fonction vectorielle :
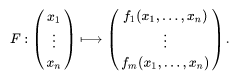
- JF(M) sa matrice jacobienne :
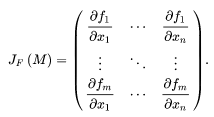
Le Jacobien correspond au déterminant de la matrice jacobienne.
4.3 Effet sur l'état de repos
Dans le modèle CP, le principe de détermination de la trajectoire d'un objet est simple. Il se résume à un seul principe.
Du
point de vue de l'objet, son état de repos est
invariant dans son propre repère  . . |
Ce qui ne signifie pas que dans le repère de la
déformation ( ) l'objet ne subit pas de variation par
rapport à sa trajectoire dans un repère euclidien
non déformé (par exemple celui de la
relativité restreinte).
) l'objet ne subit pas de variation par
rapport à sa trajectoire dans un repère euclidien
non déformé (par exemple celui de la
relativité restreinte).
Du point de vue du repère externe  , la trajectoire de
l'objet subit une variation sous la forme d'une
accélération (
, la trajectoire de
l'objet subit une variation sous la forme d'une
accélération (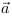 ). Cette variation correspond au
changement de trajectoire que doit subir l'objet afin que son
état de repos local reste invariant dans
). Cette variation correspond au
changement de trajectoire que doit subir l'objet afin que son
état de repos local reste invariant dans  .
.
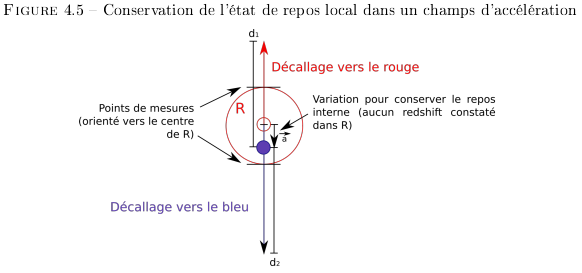
Dans la Figure 4.5, les distances 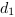 et
et 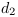 doivent être
égales. Ce qui permet de déterminer le point
à atteindre (disque bleu) pour conserver l'état
local de repos de
doivent être
égales. Ce qui permet de déterminer le point
à atteindre (disque bleu) pour conserver l'état
local de repos de  . Ce qui permet de déterminer
l'accélération
. Ce qui permet de déterminer
l'accélération 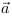 , du point de vue de
, du point de vue de  ,
de l'objet pour conserver son état de repos local.
Accélération qui, dans le repère
,
de l'objet pour conserver son état de repos local.
Accélération qui, dans le repère  , va modifier la
trajectoire de l'objet.
, va modifier la
trajectoire de l'objet.
Dans le système standard de mesures, la vitesse se
détermine par 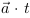 . Dans le système CP, la
vitesse correspond au Taux de Transitions (
. Dans le système CP, la
vitesse correspond au Taux de Transitions (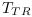 ). Elle se calcul
depuis la variation du taux de transtions (
). Elle se calcul
depuis la variation du taux de transtions (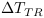 ) et du
nombre de transitions (
) et du
nombre de transitions (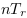 ) sur lequel cette variation intervient. La
plus petite unité de temps correspondrait à
) sur lequel cette variation intervient. La
plus petite unité de temps correspondrait à 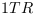 (1 transition). L'équivalent dans le système
standard correspond au temps de Planck (
(1 transition). L'équivalent dans le système
standard correspond au temps de Planck (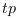 ). En distance,
celà correspond à la longueur de Planck (
). En distance,
celà correspond à la longueur de Planck (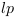 ).
).
A partir de là, il devient possible de déterminer
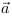 et
et 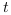 pour calculer la vitesse
pour calculer la vitesse 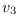 après une transition (
après une transition (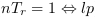 ).
).
L'idée est de déterminer
l'accélération nécessaire 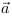 pour compenser le redshift
due à la déformation gravitationnelle. Pour
celà, il faut convertire le redshift en une vitesse
pour compenser le redshift
due à la déformation gravitationnelle. Pour
celà, il faut convertire le redshift en une vitesse 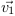 qui donnerait la valeur du redshift. De cette vitesse (
qui donnerait la valeur du redshift. De cette vitesse (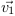 ) nous en
déduirons une accélération (
) nous en
déduirons une accélération (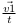 ). Tout ceci dans le
système CP qui est discret. Ce qui facilite les calculs.
). Tout ceci dans le
système CP qui est discret. Ce qui facilite les calculs.
Les EC. 11, 12 et 13 en annexes décrivent le processus de calcul.
Ce qui amène l'équation (4.16) 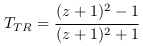 . Avec
. Avec 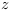 le redshift.
le redshift.
L'équation 4.16 indique la vitesse que doit
posséder le repère émetteur ( ) dans le repère
externe (
) dans le repère
externe ( )
pour que
)
pour que  ne constate pas de redshift. Mais celà ne
représente pas l'accélération qu'il subit
du point de vue du repère de la déformation
spatiale au sein duquel il évolue.
ne constate pas de redshift. Mais celà ne
représente pas l'accélération qu'il subit
du point de vue du repère de la déformation
spatiale au sein duquel il évolue.
L'intérêt du système des Cellules de Planck
est "qu'une unité de temps" correspond à une
transition. Le taux de transitions se mesure par rapport
à une unité de temps (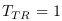 ).
).
L'EC. 14 en annexe décrivent la détermination de la variation du taux de transitions selon la variation du redshift.
Ce qui amène l'équation 4.20 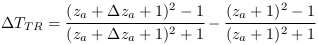 . Avec
. Avec 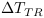 = variation du taux de transitions,
= variation du taux de transitions, 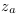 = redshift initial et
= redshift initial et 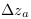 = variation du redshift initial.
= variation du redshift initial.
La Figure 4.6 issue de l'équation 4.20 montre
l'évolution du 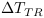 en fonction de la
variation du redshift
en fonction de la
variation du redshift 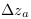 .
.
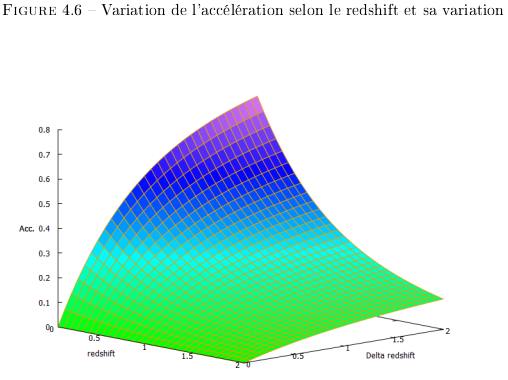
Nous constatons que 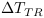 (axe Acc. sur la Figure)
augmente selon la variation du redshift (axe Delta redshift).
Mais que cette accélération diminue lorsque la
vitesse se rapproche de celle de la lumière. La vitesse
ne pouvant pas dépasser celle de la lumière (
(axe Acc. sur la Figure)
augmente selon la variation du redshift (axe Delta redshift).
Mais que cette accélération diminue lorsque la
vitesse se rapproche de celle de la lumière. La vitesse
ne pouvant pas dépasser celle de la lumière (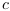 ,
,
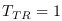 ). Attention ces observations sont
effectuées depuis le repère externe
). Attention ces observations sont
effectuées depuis le repère externe  de la déformation
gravitationnelle.
de la déformation
gravitationnelle.
4.4 Mise en correspondance des référentiels locaux
Nous avons vu les effets de la déformation sur la trame de l'Univers et sur l'état de repos des référentiels locaux. Maintenant abordons leur perception depuis un différents référentiels.
Zone de densité
La Figure 2.4 présente la 'densification' d'une zone de l'espace dur à l'augmentation locale du niveau d'énergie. Cette augmentation du niveau d'énergie est due à l'agrégation de matière par la déformation de l'espace-temps. Cette déformation amène la gravitation.
Cette déformation est créée par la scission des Cellules de Planck qui amène la création d'un puit gravitationnel. Du puit gravitationnel, les effets de la gravitation se manifstent.
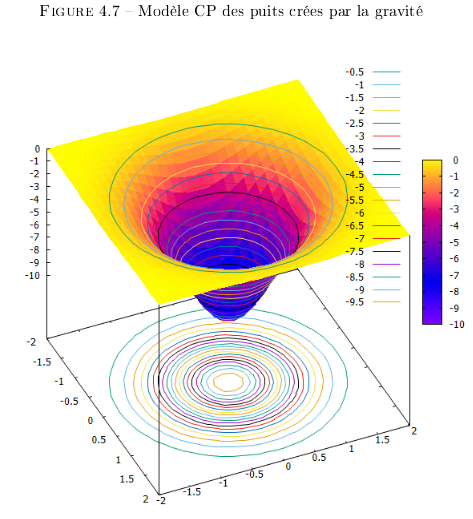
La Figure 4.7 montre une approximation des effets d'un puit de
gravité. Le puit est simulé à l'aide de la
fonction exponentielle négative 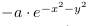 . Les lignes de niveau du puit ne sont pas
à égale distance les unes des autres (c'est une
approximation), mais à égale différence de
hauteur les unes des autres. Avec cette approximation, nous
constatons que la projection des courbes de niveau dans le plan
les rapproche les unes des autres en direction du centre du
puit. C'est le phénomène de 'densification'
constaté depuis le repère
. Les lignes de niveau du puit ne sont pas
à égale distance les unes des autres (c'est une
approximation), mais à égale différence de
hauteur les unes des autres. Avec cette approximation, nous
constatons que la projection des courbes de niveau dans le plan
les rapproche les unes des autres en direction du centre du
puit. C'est le phénomène de 'densification'
constaté depuis le repère  de l'observateur externe
au puit de gravité. C'est le phénomène de
'densification' de la zone vue avec les propriétés
des Cellules de Planck (cf. Figure
2.4).
de l'observateur externe
au puit de gravité. C'est le phénomène de
'densification' de la zone vue avec les propriétés
des Cellules de Planck (cf. Figure
2.4).
Dans le référentiel local au repos de
l'observateur, la densité de sa zone d'espace
immédiate est de 1. C'est à dire, que le vecteur
de pente de son espace local est de 0 (pour lui). En simplifiant
le repère en 2 dimensions et en considérant que
l'axe des  pointe vers le centre de la déformation, signifie que le
vecteur
pointe vers le centre de la déformation, signifie que le
vecteur  a pour composantes
a pour composantes 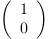 dont la longueur
est de 1 (
dont la longueur
est de 1 (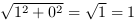 ). La mesure de la densité
perçue provient de la projection des longueurs de la
pente du puit dans le référentiel de l'observateur
et selon le repère de l'observateur. Dans le
repère de l'observateur,
). La mesure de la densité
perçue provient de la projection des longueurs de la
pente du puit dans le référentiel de l'observateur
et selon le repère de l'observateur. Dans le
repère de l'observateur, 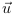 a pour
composantes
a pour
composantes 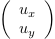 . Et
. Et 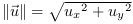 .
.
l'EC. 15, en annexes, présente la détermination de la densité par l'approche vectorielle.
De l'EC. 15
nous obtenons l'équation 4.24 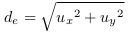 qui nous
donne la densité perçue du repère de
l'observateur.
qui nous
donne la densité perçue du repère de
l'observateur.
l'EC. 16,
en annexes, présente la même chose, mais avec
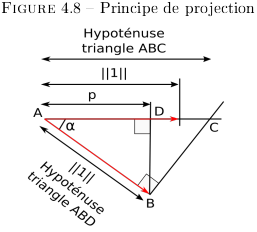
l'approche tangentielle. Le principe de l'approche tangentielle
est présenté sur la Figure 4.8. Avec 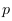 la projection de la norme
(hypothénuse du triangle ABD = tangente
étudiée) du repère observé dans le
repère de l'observateur.
la projection de la norme
(hypothénuse du triangle ABD = tangente
étudiée) du repère observé dans le
repère de l'observateur. 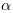 l'angle de la
pente (tangente)du puit vu du reprère de l'observateur.
Ceci faisant le lien avec l'inclinaison d'un repère en
mouvement par rapport à un autre repère dans le
cadre d'un mouvement rectiligne uniforme (cf. Figure 3.9, Compatibilité
avec la relativité restreinte, Vision
relative entre repères différents).
l'angle de la
pente (tangente)du puit vu du reprère de l'observateur.
Ceci faisant le lien avec l'inclinaison d'un repère en
mouvement par rapport à un autre repère dans le
cadre d'un mouvement rectiligne uniforme (cf. Figure 3.9, Compatibilité
avec la relativité restreinte, Vision
relative entre repères différents).
L'EC. 16
nous donne l'équation 4.28 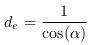 , qui
correspond à l'équation
4.24 de l'approche vectorielle. De la même
façon, l'EC. 17
détermine l'équation 4.33
, qui
correspond à l'équation
4.24 de l'approche vectorielle. De la même
façon, l'EC. 17
détermine l'équation 4.33 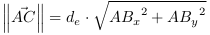 , selon
l'approche par composition de vecteurs.
, selon
l'approche par composition de vecteurs.
Cette valeur de densité 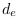 est importance car elle permet de
traduire la déformation d'un puit gravitationnel en
distance (
est importance car elle permet de
traduire la déformation d'un puit gravitationnel en
distance (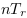 )
perçue par l'observateur.
)
perçue par l'observateur.
Elle permet, aussi, de déterminer les contraintes sur le référentiel de l'observateur pour être transposé dans le référentiel observé.
De façon indépendante, nous avons vu comment la variation d'énergie au sein d'une sphère provoquant la création de CP (cf. Equation 2.7, Propriétés de CP, Taux de transition et taux de création). Nous venons de voir l'expression de la densité (cf. équations 4.24, 4.28).
EC. 18, en annexes, fait le lien entre la densité dss CP et la variation du rayon de la sphère liée à la variation d'énergie.
Contraintes de transpositions
La projection selon le repère observé montre la déformation subit par le repère de l'observateur pour y passer. Nommons cela la transposition du repère de l'observateur dans le repère observé qui est déterminé par le puit gravitationnel (cf. Figure 4.9). Ces différences entre repères se traduisent en contraintes pour passer d'un repère à l'autre. Dans la Figure 4.9, les projections verticales, perpendiculaires au repère de l'observateur, montrent sa perception de la 'densification' de l'espace. Les projections perpendiculaires selon le repère du puit de gravité (en rouge), montrent les déformations que subirait le repère de l'observateur pour se transposer dans le repère du puit de gravité.
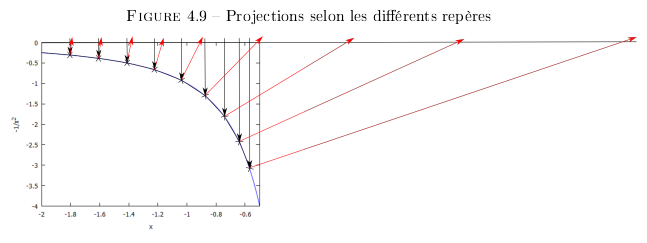
C'est de ces contraintes qu'apparait l'effet d'étirement et les forces de marées lors du rapprochement d'un important puit de gravité.
L'EC. 19, en annexes, présente la détermination de la projection depuis le puit gravitationnel par rapport à le 'densité' de celui-ci.
En se référent à la Figure 4.8, l'équation
4.46 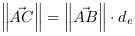 (détermine dans l'EC. 19) montre la corrélation entre
la déformation et les contraintes de transposition avec
la 'densité' d'un puit de gravité.
(détermine dans l'EC. 19) montre la corrélation entre
la déformation et les contraintes de transposition avec
la 'densité' d'un puit de gravité.
Grace à l'EC. 19 et l'équation 4.46 nous venons de démontrer l'importance de cette notion de 'densité' qui permet de réaliser les transpositions entre les différents repères.
Déformations convexes et concaves
Jusqu'à maintenant, nous avons vu un seul type de déformation. Nous avons déterminé la déforamtion convexe qui mène à des contraites divergentes lors de la transposition dans des référentiels successifs d'un puit de gravité.
Il existe un autre type de déformations. Les déformations convexes. Ces déformations mènent à des contraintes convergentes (cf. Figure 4.3). C'est de ce type de déformations que viennent les contraintes latérales sur le repère de l'observateur.
La Figure 4.10 présente les deux types de déformations ainsi que leurs effets. La déformation convexe est symbolisée par la courbe noire. Ses effets par les vecteurs noirs. Ils divergent. La déformation concave est symbolisée par la courbe rouge. Ses effets par les vecteurs rouges. Ils convergent.
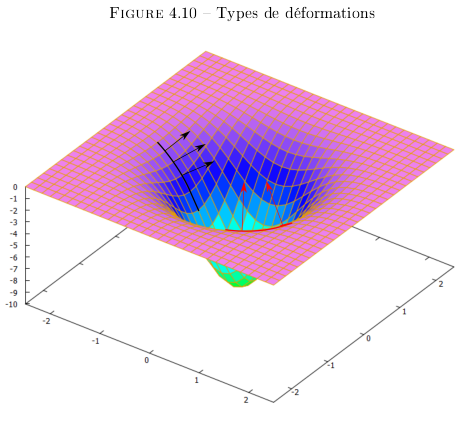
4.5 L'expansion une illusion ou une réalité ?
L'augmentation de 'densité' (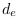 )d'une zone
d'espace-temps à l'approche d'un puit de gravité
jouerait sur la perception des distances (
)d'une zone
d'espace-temps à l'approche d'un puit de gravité
jouerait sur la perception des distances (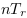 ).
).
Par exemple lorsqu'entre un pulsar et l'observateur
s'interposerait un puit de gravité, la densification de
l'espace-temps serait perçue comme un alongement des
distances. Ceci du fait qu'entre chaque ligne de niveau de la
Figure 4.11, il y aurait le même nombre de transitions 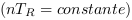 .
.
Ainsi pour un pulsar, dont la trajectoire de l'observateur intercalerait une zone de 'densité', il serait constaté un alongement des distances et un déplacement rapide du pulsar. Lorsque le pulsar commencerait à passer derrière la zone de densité, la mesure du rythme des pulsations diminuerait. Un déplacement à l'opposé du puit de gravitation serait également observé. Cela proviendrait simplement du fait que l'observateur voit son référentiel comme un référentiel Euclidien orthonormé.
La Figure 4.11 montre le mirage gravitationnel observé qui serait due à la zone de densité qui s'intercalerait entre le pulsar et l'observateur. Sur la figure, les étoiles du côté de l'observateur indique les positions de mesures. Sur le premier schéma est représenté est représenté le parcours du signal en provenance du pulsar. Le second schéma projette les observation dans le repère Euclidien orthonormé de l'observateur.

4.6 La lumière étalon Universel ?
De part la relativité restreinte, nous savons que 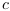 , la
vitesse de la lumière, est invariante quelque soit le
repère d'observation.
, la
vitesse de la lumière, est invariante quelque soit le
repère d'observation.
Mais sa fréquence ne serait-elle pas un invariant dans son propre référentiel ? La variation de fréquence entre le repère de l'émetteur et celui du recepteur viendrait des effets relativistes. Avec les contraintes de transpositions, l'observateur ne mesurerait-il qu'une fréquence propre à son référentiel ?
Par exemple, admettons une fréquence émise de 4
hertz dans le référentiel 1 ( ). Elle serait
mesurée à 8 hertz dans le
référentiel 2 (
). Elle serait
mesurée à 8 hertz dans le
référentiel 2 ( ) si
) si 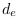 = 2.
= 2.
Comme le montre la Figure 4.12, la fréquence de 4 hertz
émise depuis  serait mesurée 8 hertz dans le
repère
serait mesurée 8 hertz dans le
repère  . Ceci non pas que la fréquence ait
changé en elle-même.
. Ceci non pas que la fréquence ait
changé en elle-même.
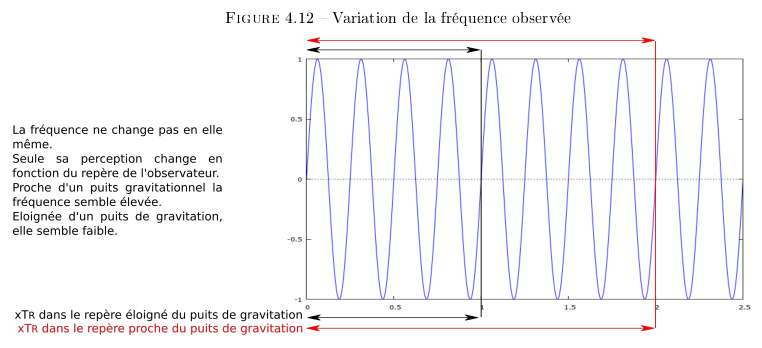
Rappelons, comme nous l'avons vu précédemment,
que la transposition d'un repère à un autre
repère amène des contraintes. Dans  la flèche noire du
graphique représente la norme de ce repère. A
l'identique, la flèche rouge représente la norme
du repère
la flèche noire du
graphique représente la norme de ce repère. A
l'identique, la flèche rouge représente la norme
du repère  . En soit, la fréquence n'a pas
changé. Mais la norme
. En soit, la fréquence n'a pas
changé. Mais la norme 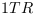 qui servirait d'unité de
mesure n'engloberait pas le même volume d'espace-temps
d'un repère à l'autre (comparaison entre les deux
repère. C'est l'étalon de mesure qui
évoluerait et non le phénomène
mesuré qui varierait). Pourtant, dans chaque
repère les propriétés observées des
CP resteraient les mêmes et le rapport dans le
système de mesures standard
qui servirait d'unité de
mesure n'engloberait pas le même volume d'espace-temps
d'un repère à l'autre (comparaison entre les deux
repère. C'est l'étalon de mesure qui
évoluerait et non le phénomène
mesuré qui varierait). Pourtant, dans chaque
repère les propriétés observées des
CP resteraient les mêmes et le rapport dans le
système de mesures standard 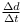 resterait le même (cf. équation 1.1, EC. 1 en annexes) et égale à
resterait le même (cf. équation 1.1, EC. 1 en annexes) et égale à 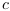 .
.
4.7 Variation de l'énergie des CP
L'apparition des puits de gravité vient de la création de CP afin de conserver une densité d'énergie constante. Ceci provenant de l'apport d'énergie locale due à l'accrétion de matière. Mais si l'énergie de chaque CP de cette zone ne changeait pas, le bilan énergétique ne serait pas nul.
Reprenons l'équation 2.4 vue dans l'EC. 4 en annexes 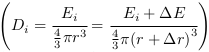 .
Considérons que
.
Considérons que 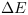 corresponde à l'apport
d'énergie due à la matière qui
s'agrège. En décomposant
corresponde à l'apport
d'énergie due à la matière qui
s'agrège. En décomposant 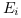 en énergie de la
matière
en énergie de la
matière 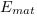 et en énergie des CP
et en énergie des CP 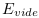 , nous pouvons
montrer (cf. EC. 20 en annexes) que le rapport entre
l'énergie de chacune des CP contenue dans la nouvelle
sphère de rayon (
, nous pouvons
montrer (cf. EC. 20 en annexes) que le rapport entre
l'énergie de chacune des CP contenue dans la nouvelle
sphère de rayon (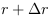 )
diminue par rapport à l'énergie totale contenue
dans la sphère.
)
diminue par rapport à l'énergie totale contenue
dans la sphère.
Nous obtenons l'équation 4.49 qui exprime
l'énergie du vide 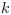 par rapport à
l'énergie de la matière :
par rapport à
l'énergie de la matière :
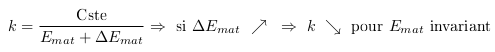
Cette équation nous montre que si
l'énergie liée à la matière
augmente, celle liée au vide (CP) diminue. Comme nous
l'avons vu avec l'équation 2.7 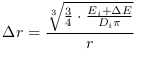 (cf. EC. 4 en annexe), le rayon de la zone de
densité augmente. De ce fait l'énergie moyenne des
CP diminue.
(cf. EC. 4 en annexe), le rayon de la zone de
densité augmente. De ce fait l'énergie moyenne des
CP diminue.
Maintenant, si nous considérons une diminution du niveau global d'énergie, en appliquant les mêmes principes, constaterions une diminution du nombre de CP. Donc ces zones d'où se retirerait la matière engendreraient de faibles densités. Et ces zones de faibles densité raccourciraient les distances par rapport aux zones à plus forte densité. Et à l'opposé des zones de densité, elles s'élèveraient au dessus du niveau moyen (inclinaison opposée à celle des puits de gravités) pour former des 'anti' puits de gravité. Avec l'inclinaison, l'effet serait de 'pousser' la matière en dehors de ces zones de faible énergie et de faible densité. Ce qui expliquerait le grand répulseur (Dipole Repeller) qui pousse notre galaxie vers le grand attracteur de Shapley.
C'est typiquement ce qui pourrait se passer lorsque la matière passerait d'une zone au puit de gravité. Dans ce cas, la zone d'où viendrait la matière verrait sa densité diminuer, et selon le principe de l'équation 2.7, les CP fusionneraient afin de conserver une niveau d'énergie local constant.
A un tel phénomène s'ajouterait celui du transfert d'énergie des CP les plus énergétiques vers les CP les moins énergétiques.
4.8 Régime énergétique
Le principe serait que le niveau d'énergie des CP tends à se régulariser entre chaque CP adjacentes. Le niveau total d'énergie resterait constant conformément au premier principe de la thermodynamique3. Les CP les plus énergétiques cèderaient leur énergie aux moins énergétiques. Conserver le niveau total d'énergie impliquerait que le niveau des CP les plus énergétiques diminuerait, alors que celui des CP les moins énergétiques augmenterait. Cette description s'inspire de la diffusion de chaleur au sein d'un milieu selon la loi de Fourier4.
Selon ce principe, considérons 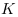 la conductance du
système étudié. Avec
la conductance du
système étudié. Avec 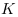 inclus dans l'encadrement
inclus dans l'encadrement
![[0..1] [0..1]](images/EQ/encadrement-0-1.png) .
.
Si nous considérons 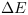 la différence
d'énergie entre 2 ensembles
la différence
d'énergie entre 2 ensembles 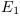 et
et 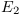 de CP.
de CP.
Avec :
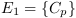 ;
;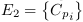 ;
;  le
bilan des flux d'énergie entre
le
bilan des flux d'énergie entre 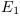 et
et 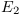 .
.

Les EC. 21 et 22 en annexes posent le régime d'échange d'énergie entre les CP.
L'équation 4.58 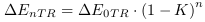 (cf. EC. 22) indique le
gradient d'énergie en partant d'une CP initiale
jusqu'à la n (ième) CP.
(cf. EC. 22) indique le
gradient d'énergie en partant d'une CP initiale
jusqu'à la n (ième) CP.
L'équation 4.60 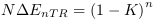 (cf. EC. 22) normalise le
gradient d'énergie de l'équation 4.58. Ainsi elle
s'exprime sans référence à la variation
d'énergie initiale. Le gradient peut être
déterminé depuis l'équation 4.60. Il
suffira de le multiplier par la valeur de la variation
d'énergie intiale.
(cf. EC. 22) normalise le
gradient d'énergie de l'équation 4.58. Ainsi elle
s'exprime sans référence à la variation
d'énergie initiale. Le gradient peut être
déterminé depuis l'équation 4.60. Il
suffira de le multiplier par la valeur de la variation
d'énergie intiale.
La Figure 4.15 montre l'évolution de la
différence d'énergie entre CP selon 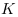 , la conductance
d'énergie entre CP et TR le nombre de transitions entre
CP.
, la conductance
d'énergie entre CP et TR le nombre de transitions entre
CP.
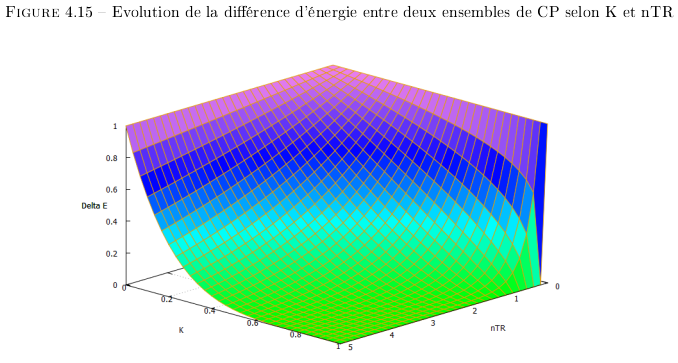
Nous constatons que plus 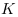 est proche de 0 et plus il faut de
transitions (
est proche de 0 et plus il faut de
transitions (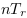 ) pour réaliser l'harmonisation
d'énergie. La formule étant de la forme
) pour réaliser l'harmonisation
d'énergie. La formule étant de la forme 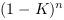 avec
avec 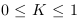 ,
si
,
si 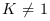 et
et 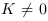 ,
alors il faut
,
alors il faut 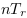 transitions avec
transitions avec 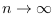 .
Et si
.
Et si 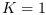 , alors
, alors 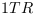 suffit pour harmoniser les
niveaux d'énergie. Si
suffit pour harmoniser les
niveaux d'énergie. Si 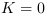 , il n'y a pas
d'harmonisation d'énergie.
, il n'y a pas
d'harmonisation d'énergie.
L'EC. 23 en annexes, vérifie le respect du premier principe de la thermodynamique.
Avec l'équation 4.49, nous avons constaté que l'énergie d'une zone de CP diminuait et que cette variation était inversement proportionnelle à la variation de la densité de la zone.
Maintenant, si nous considérons une CP à la frontière d'une zone de densité avec le reste de l'espace-temps, nous constatons que le niveau d'énergie des CP à l'extérieur de la zone de densité est supérieur à celui des CP à l'intérieur de la zone de densité.
Avec ce que nous venons de voir sur le régime énergétique des CP, il devrait y avoir un flux d'énergie des CP externes à la zone vers les CP internes à la zone. Par récurrence nous pouvons vérifier le même mécanisme vers des CP d'une zone plus dense. Et plus nous nous rapprochons du puit de gravité et plus la densité devient importante (cf. équations 4.24 et 4.28).
Ce qui nous amène à définir le gradient
d'énergie 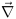 comme un gradient partant de l'extérieur de la zone de
densité vers son centre.
comme un gradient partant de l'extérieur de la zone de
densité vers son centre.
Si nous reprenons l'équation 2.7 qui détermine le
rayon d'une sphère de densité selon la variation
d'énergie, alors, si la conductance d'énergie 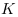 est
inférieure à 1 nous en déduisons :
est
inférieure à 1 nous en déduisons :
- L'apport d'énergie des CP externes à la zone de densité augmente le rayon de la sphère. Ce qui a pour effet d'augmenter progressivement la densité de la zone ;
- La diminution de l'énergie à l'extérieur de la zone amènerait une fusion des CP afin de conserver une densité d'énergie locale constante ;
- Cette diminution de densité à l'extérieur de la zone de densité aurait les effets d'un répulseur. Ce phénomène venant de la surélévation du voisinage du puit de gravité au dessus du niveau moyen du vide.
Une tel phénomène pourrait expliquer pourquoi la rotation des vieilles galaxies semble lié au phénomène de la matière noire. Cet effet 'répulseur' poussant l'extérieur des galaxies vers leur centre. Ce qui obligerait à avoir une rotation rapide afin de résister à cet effet de répulsion.
Les observations de jeunes galaxies (https://phys.org/news/2017-03-dark-influential-galaxies-early-universe.html) sembleraient montrer que les galaxies à fort redshift ont leur dynamique complètement dominée par la matière barionique. Alors que la dynamique des vieilles galaxies est essentiellement dominée par la matière noire.
Dans le modèle CP ce phénomène pourrait
être lié à la surélévation des
bords du puit de gravité. Mais cette dynamique
dépendrait de la conductance d'énergie (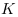 ) des CP. Plus
) des CP. Plus 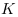 est proche de 0 et plus le
temps mis pour que s'établisse cette
surélévation serait important. Donc seules les
galaxies agées verraient leur dynamique influencée
par cette surélévation. Rappelons que cette
surélévation entraine une rotation plus importante
des zones externes des galaxies qu'avec les euls effets de la
matière normale. Pour les jeunes galaxies, cette
surélévation serait minime. Ce qui n'en
n'influencerait pas la dynamique.
est proche de 0 et plus le
temps mis pour que s'établisse cette
surélévation serait important. Donc seules les
galaxies agées verraient leur dynamique influencée
par cette surélévation. Rappelons que cette
surélévation entraine une rotation plus importante
des zones externes des galaxies qu'avec les euls effets de la
matière normale. Pour les jeunes galaxies, cette
surélévation serait minime. Ce qui n'en
n'influencerait pas la dynamique.
3 : Lors de toute transformation, il y a conservation de l'énergie.
4 : 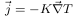 ,
avec
,
avec 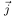 = vecteur d'intensité du courant thermique,
= vecteur d'intensité du courant thermique, 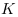 = conductivité
thermique,
= conductivité
thermique, 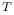 = température.
= température.
Table des matières :
- 1. Qu'est-ce qu'une Cellule de Planck (CP)
- 2. Propriétés des Cellules de Planck
- Harmonisation d'énergie, scission et fusion
- Scission et fusion
- Taux de transition et taux de création
- Unités de mesures et conversions entre modèle CP et Modèle standard
- 3. Compatibilité avec la relativité restreinte
- 4. La gravitation et l'expansion
- Corrélation entre système de mesures classique et système de mesure CP
- Principe de la déformation gravitationnelle
- Effet sur l'état de repos
- Mise en correspondance des référentiels locaux
- L'expansion une illusion ou une réalité ?
- La lumière : l'étalon universel ?
- Variation de l'énergie des CP
- Régime énergétique
- 5. Remerciements
- 6. Annexes
/!\ Attention ce document est classifié CONFIDENTIEL. Il ne peut être diffusé sans accord.

