

Auteur : Lascap Ertîamel
3. Compatibilité avec la relativité
restreinte
Le modèle CP est compatible avec la relativité restreinte. Les transformations de Lorentz s'appliquent de la même manière dans le système CP que dans le système classique.
La composition des vitesses relativistes correspond au modèle standard. Tout calcul relativiste dans un système (standard ou CP) donne le même résultat après transformation que dans l'autre système.
Les calculs semblent plus simples à effectuer dans le système CP que dans le système standard.
3.1 Vision relative entre repères
différents
Poincaré, Einstein et d'autres ont décrit la relativité. Lorentz a défini les équations de transformations entre différents repères mobiles les uns par rapport aux autres. Einstein a conçu la relativité restreinte puis la relativité générale en s'appuyant sur les travaux de Lorentz et en posant le principe d'équivalence.
Corrélation entre la relativité et les
Cellules de Planck

L'étalon de toute mesure en
relativité est la vitesse de la lumière 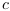 . Dans le système CP
. Dans le système CP
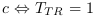 . En effectuant
une mesure de
. En effectuant
une mesure de ![[AB] [AB]](images/EQ/segmentAB.png) , l'observateur mesurerait le nombre de
transitions entre A et B (cf. Figure 3.1).
, l'observateur mesurerait le nombre de
transitions entre A et B (cf. Figure 3.1).
Nous avons vu qu'une vitesse s'exprime par rapport à
celle de 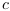 .La
vitesse de
.La
vitesse de 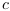 dans le système CP correspond à
dans le système CP correspond à 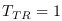 (Taux de
transition = 1). Avec le nombre de transitions
observé
(Taux de
transition = 1). Avec le nombre de transitions
observé 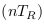 et les
propriétés des CP
et les
propriétés des CP 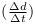 nous pourrions en déduire la distance et le temps de
parcours du signal :
nous pourrions en déduire la distance et le temps de
parcours du signal :
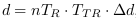 ;
;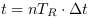 ;
; - Et avec
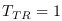 (vitesse de
(vitesse de  ) ;
) ; - Le rapport de la distance sur le temps donnerait toujours
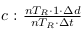 .
.
D'où 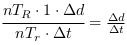 .
.
Ce qui, par définition des CP, donne 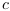 car
car 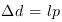 (longueur de Planck) et
(longueur de Planck) et 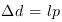 (temps de Planck) et que
(temps de Planck) et que 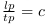 .
.
Variation des distances
Un des exemples couramment utilisé pour expliquer la
relativité fait l'analogie avec un quai et un bateau.
Dans une cabine du bateau, des personnes en mesurent la taille
avec un signal lumineux et deux autres assistent à
l'expérience depuis le quai (cf. Figure 3.2). Un bateau
n'étant pas assez rapide pour notre expérience
nous prendrons un TTTGV (Train à Très Très
Grande Vitesse). Du fait du taux de transition maximal (=1)
entre CP et qui correspondrait à 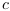 , le principe de la
relativité restreinte est respecté. Dans notre
TTTGV, une expérience mesure la taille d'un wagon
à l'aide d'un rayon lumineux. Au même moment,
à quai, des observateurs assistent à
l'expérience. La vitesse de la lumière
étant la même dans les deux repères, les
observateurs, sur la quai, trouvent que le wagon est très
long (longueur de la flèche bleue sur le quai). A
contrario, la mesure réalisée dans le TTTGV
(longueur de la flèche rouge dans le train) trouve une
longueur bien petite. La différence venant des deux
référentiels distincts (le train en mouvement par
rapport au quai et le quai fixe par rapport aux observateurs).
, le principe de la
relativité restreinte est respecté. Dans notre
TTTGV, une expérience mesure la taille d'un wagon
à l'aide d'un rayon lumineux. Au même moment,
à quai, des observateurs assistent à
l'expérience. La vitesse de la lumière
étant la même dans les deux repères, les
observateurs, sur la quai, trouvent que le wagon est très
long (longueur de la flèche bleue sur le quai). A
contrario, la mesure réalisée dans le TTTGV
(longueur de la flèche rouge dans le train) trouve une
longueur bien petite. La différence venant des deux
référentiels distincts (le train en mouvement par
rapport au quai et le quai fixe par rapport aux observateurs).

Variation du temps
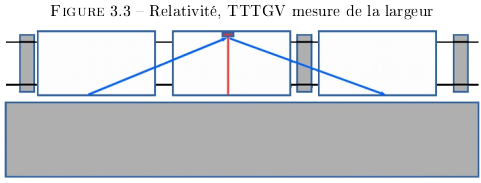
De manière similaire, dans un autre wagon, une autre expérience se déroule. Cette fois, il s'agit de mesurer la largeur du wagon (cf. Figure 3.3). Dans le wagon, fait juste un allé/retour (trait rouge sur le schéma).
Par contre pour les observateurs sur le quai, la lumière
effectue un trajet bien plus long (traits bleus). Ce qui
amène à mesurer un écoulement
différent du temps puisque le rapport des distances et du
temps entre le référentiel du TTTGV et le quai
donnent 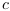 .
.
Perte de simultanéité
Dans un des wagons du TTTGV, le train à l'arret (même référentiel que le quai), un mur a été positionné en son milieu (cf. Figure 3.4). Un rayon est envoyé simultanément vers l'arrière et vers l'avant du wagon. A l'arrêt, dans le train comme sur le quai, les deux rayons ateignent les extrémités du wagon simultanément. Mais lorsque le TTTGV roule, il y a perte de simultanéité entre les mesures faitent dans le train et celles perçues depuis le quai. Alors que dans le train, il n'y a pas perte de simultanéité, depuis le quai le rayon atteint l'arrière du wagon plus tôt que celui qui atteint l'avant du wagon. Les CP sont compatibles avec la relativité restreinte.

Le problème semble venir de l'intérieur du train lui-même (traits rouges) avec le maintien de la simultanéité train à l'arrêt et train en mouvement. Car comment expliquer que dans le train en mouvement, les deux rayons touchent leur parois simultanément ? Du point de vue du train en mouvement, la distance et le temps doivent être invariants entre l'avant et l'arrière que le train soit ou non en mouvement.
Déformation de l'onservation et inclinaison du plan spatio-temporel
Le paradoxe de la simultanéité à l'intérieur du train vient de la perception que nous en avons depuis le quai et de la conversion en distance et temps de CP.
Au sein de la trame des Cellules de Planck depuis le quai (cf. Figure 3.5) :
- La ligne bleue montre la progression des transitions dans le sens du mouvement ;
- La ligne rouge montre la progression des transitions dans le sens inverse à celui du mouvement ;
- La ligneverte indique le mouvement du wagon depuis son milieu ;
- L'intersection entre la courbe bleue et la verte indiquerait le nombre de transitions pour atteindre la paroi avant du wagon ;
- L'intersection entre la courbe rouge et la courbe verte indiquerait le nombre de transitions pour atteindre la paroi arrière du wagon.
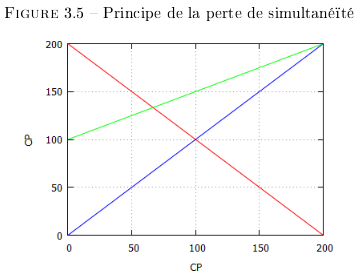
Pour une longueur du wagon de 100CP et une vitesse de 0,5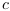 (la moitié de la
vitesse de la lumière) et à partir du point
d'émission, il y aurait environ 200 transitions pour
atteindre la paroi avant. Il n'y en aurait que 66 pour atteindre
la paroi arrière. Pourtant, les mesures effectuées
à l'intérieur du train sont identiques entre
l'avant et l'arrière. La vitesse de déplacement du
train jouerait sur la conversion ? Ainsi le taux de conversion
serait de
(la moitié de la
vitesse de la lumière) et à partir du point
d'émission, il y aurait environ 200 transitions pour
atteindre la paroi avant. Il n'y en aurait que 66 pour atteindre
la paroi arrière. Pourtant, les mesures effectuées
à l'intérieur du train sont identiques entre
l'avant et l'arrière. La vitesse de déplacement du
train jouerait sur la conversion ? Ainsi le taux de conversion
serait de 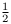 dans le sens du déplacement et
de
dans le sens du déplacement et
de 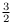 dans le sens opposé.
dans le sens opposé.
Avant le départ du train l'expérience a été menée. Du milieu à chacune des extrémités du wagon, les mesures indiquaient 100.d (distance) et 100.t (temps). En réalisant l'expérience en roulant, de telles mesures ne changeraient pas. Par contre depuis le quai seraient mesuré 66.d et 66.t vers l'arrière et 200.d et 200.t vers l'avant(cf. EC. 5).
En appliquant les conversions nous obtenerions les mesures avant et arrière :
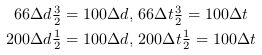
- La corrélation entre les deux repères est assurée ;
- La vitesse de la lumière est inchangée.
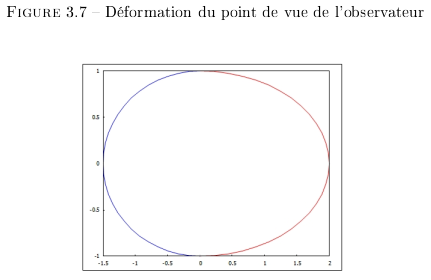
La déformation (cf. Figures 3.6 et 3.7) ne provient que de la comparaison entre les deux repères. Seul l'observateur, depuis son repère constate un changement dans la simultanéité dans le repère en mouvement qu'il observe.
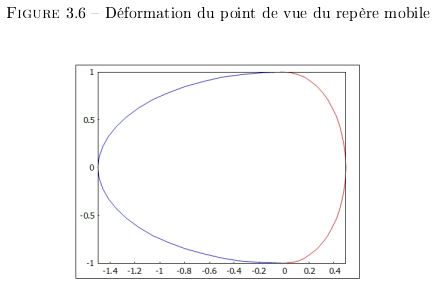
Notice :
- Rouge : Sens du déplacement ;
- Bleu : Senns opposé au déplacement ;
- En face, un angle de 0° par rapport au déplacement, la déformation est importante ;
- Derrière, un angle de 180° par rapport au déplacement, la déformation est importante ;
- En bas et en haut 90°, -90°, il n'y a pas de déformation.
Vu autrement, le déplacement modifie la projection d'un repère observé dans celui de l'observateur. Il ne s'agit que d'une transposition géométrique entre deux repères en mouvements. La Figure 3.8 montre les différences entre les projections dans le sens du mouvement et dans le sens opposé. Le repère du bas montre la vision du parcours du signal dans le sens du mouvement. Celui du dessus montre le parcours dans le sens opposé au mouvement.
La différence entre ces deux projections modélise les observations réalisées sur le quai et dans le train.
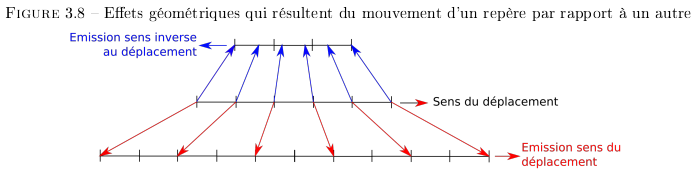
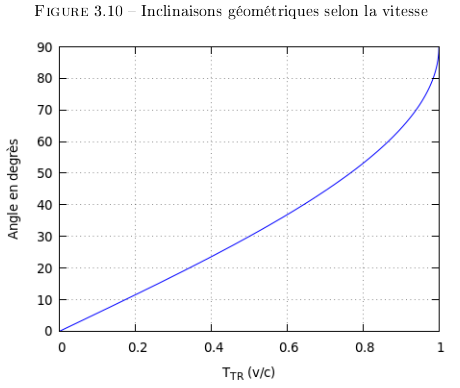
Pourtant le nombre de transitions vers l'avant et vers l'arrière dans le train ne change pas si le train est au repos ou en mouvement. D'un point de vue géométrique cet écart s'explique par une inclinaison du repère spatio-temporel du train par rapport au quai. Le plan de l'espace-temps du train s'incline par rapport à celui du quai selon sa vitesse. Les différences de mesures ne viennent que des projections du repère en mouvement dans le repère des observateurs sur le quai (cf. Figure 3.9). Ce qui permet de définir la courbe d'inclinaison par rapport à la vitesse du la Figure 3.10. Avec une inclinaison de 90°, les deux repères sont disjoints et plus aucune information ne peut transiter entre les deux repères.
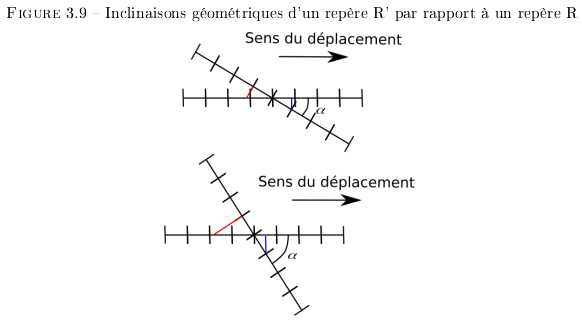
L'inclinaison amène la conservation du nombre et des caactéristiques des CP dans le repère en mouvement observé par rapport à celui de l'onservateur. Sur les schémas de la Figure 3.9, les traits bleus démontrent la projection qui amène une réduction apparante du nombre de CP depuis l'observateur pour expliquer la perte de simultanéité observée. Et les traits rouges démontrent la projection qui amène une augmentation apparante du nombre de CP depuis l'observateur pour expliquer la perte de simultanéité.
3.2 Transformations de Lorentz
Les transformations de Lorentz sont de la forme 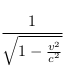 ou
ou 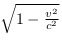 . Elles
définissent la conversion à réaliser pour
mesurer l'observation d'un repère depuis un autre
repère. Elles décrivent les variations de
longueurs et de temps relatives entre deux repères
distincts mobiles l'un par rapport à l'autre.
. Elles
définissent la conversion à réaliser pour
mesurer l'observation d'un repère depuis un autre
repère. Elles décrivent les variations de
longueurs et de temps relatives entre deux repères
distincts mobiles l'un par rapport à l'autre.
Taux de transition
Avec le modèle des Cellules de Planck, la notion
classique de vitesse laisse la place à celle de Taux de
Transition 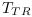 . La notion de Taux de Transition
définirait le rythme de transition entre CP. Avec
. La notion de Taux de Transition
définirait le rythme de transition entre CP. Avec 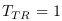 , le rythme serait maximum. Il correspondrait
à
, le rythme serait maximum. Il correspondrait
à 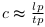 . Le conversion du taux de
transition permettrait de spécifier une vitesse
relativement à
. Le conversion du taux de
transition permettrait de spécifier une vitesse
relativement à 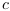 (vitesse de la lumière).
(vitesse de la lumière).
Par exemple 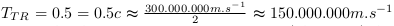 . La vitesse viendrait de la conversion du
taux de transition selon les caractéristiques
mesurées (observées) des Cellules de Planck (cf. Qu'est-ce
qu'une Cellule de Planck (CP)).
. La vitesse viendrait de la conversion du
taux de transition selon les caractéristiques
mesurées (observées) des Cellules de Planck (cf. Qu'est-ce
qu'une Cellule de Planck (CP)).
Donc 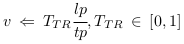 dans
dans  .
Dans une direction donnée, le taux de transition pourrait
prendre toutes les valeurs entre 0 et 1. 0 = pas de vitesse. 1 =
vitesse de la lumière.
.
Dans une direction donnée, le taux de transition pourrait
prendre toutes les valeurs entre 0 et 1. 0 = pas de vitesse. 1 =
vitesse de la lumière.
Equivalence vitesse / taux de transition dans les transformations de Lorentz
Les formules des transformations de Lorentz s'appuient sur le
carré de la vitesse 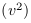 et le
carré de la vitesse de la lumière
et le
carré de la vitesse de la lumière 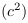 . Avec les
taux de transition, il y a une équivalence implicite avec
. Avec les
taux de transition, il y a une équivalence implicite avec
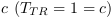 (cf. EC. 6).
(cf. EC. 6).
Le modèle à base de Cellules de Planck est
compatible avec les transformations de Lorentz sur lesquelles
s'appuie la relativité restreinte. Indifféremment,
il est possible le taux de transition ou sa convertion dans le
système standard 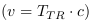 pour déterminer les variations de distance, de temps et
de masse.
pour déterminer les variations de distance, de temps et
de masse.
Correspondance des transformées de Lorentz entre le système standard et le système CP :
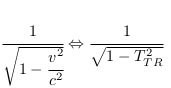
Application des transformées de Lorentz dans le modèle CP
Dans l'Univers des CP, il n'y a directement ni espace, ni temps. Ces notions sont observées lors des mesures. Par conséquent, les calculs doivent s'effectuer sans rapport avec l'espace et le temps. Seules les transformations en fin de processus doivent amener les notions d'espace (distance) et de temps.
Dans les sections à venir, les notations suivantes sont utilisées :
- Nombre de transitions :
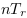 ;
; - Taux de transitions :
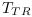 ;
; - Variation du taux de transitions :
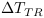 .
.
Transformations avec un repère en mouvement uniforme
Dans le modèle CP, il n'y a pas de notions de distance, de temps et de vitesse. Il y a les notions de transitions (nombre de transitions), et de taux de transitions. Le taux de transition d'un objet, d'une particule, dans le modèle CP s'exprime par rapport au taux de transitions maximum :
- Le taux de transitions maximum correspond à celui de la lumière et est égal à 1 ;
- Le taux de transitions d'un objet ou d'une particule est un rationnel positif allant de 0 à 1 ;
- 0 pas de taux de transition (objet ou particule immobile par rapport au référentiel de l'observateur ;
- 1 vitesse de la lumière par rapport au référentiel de l'observateur.
Conversion des distances et du temps : Si avec
les CP, il n'y a pas de notion de vitesse, il n'y a pas de
notion de distances, il n'y a pas la notion de temps. Par
contre, il y a les notions d'énergie et de taux de
transitions. Posons que l'énergie d'un système
notée 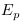 et son énergie potentielle
(perçue depuis un autre référentiel)
notée
et son énergie potentielle
(perçue depuis un autre référentiel)
notée 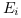 .
Il est à noter que cette 'transformation'
d'énergie est le pendant de la transformation de la masse
.
Il est à noter que cette 'transformation'
d'énergie est le pendant de la transformation de la masse
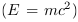 . Cette notion doit
être conservée à l'esprit au moment des
conversions en distances et en temps.
. Cette notion doit
être conservée à l'esprit au moment des
conversions en distances et en temps.
EC. 7 (en annexes) vérifie qu'avec les conversions, nous retrouvons bien l'équivalent du modèle standard, après application des transformations de Lorentz dans le modèle CP.
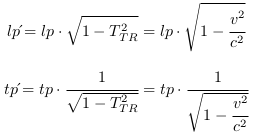
Avec :
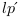 : projection de la longueur de Planck du
référentiel observé dans celui de
l'observateur ;
: projection de la longueur de Planck du
référentiel observé dans celui de
l'observateur ;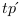 : projection du temps de Planck du référentiel
observé dans celui du l'observateur ;
: projection du temps de Planck du référentiel
observé dans celui du l'observateur ;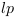 :
longueur de Planck dans le référentiel
observé ;
:
longueur de Planck dans le référentiel
observé ;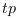 :
temps de Planck dans le référentiel
observé ;
:
temps de Planck dans le référentiel
observé ;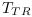 : Vitesse du
référentiel observé par rapport à
celui de l'observateur.
: Vitesse du
référentiel observé par rapport à
celui de l'observateur.
Conversion des vitesses : Pour montrer la cohérence du modèle CP avec le modèle classique l'EC. 8 (en annexes) part de la composition des vitesses colinéaires (vitesses de directions parallèles) du modèle classique.
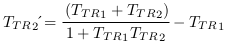
Avec :
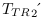 : Projection de
: Projection de 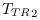 , mesuré
dans
, mesuré
dans  le référentiel
observé, dans le réferentiel
le référentiel
observé, dans le réferentiel  de l'observateur ;
de l'observateur ;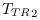 :
Vitesse mesurée dans
:
Vitesse mesurée dans  ;
;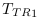 :
Vitesse relative de
:
Vitesse relative de  par rapport à
par rapport à  .
.
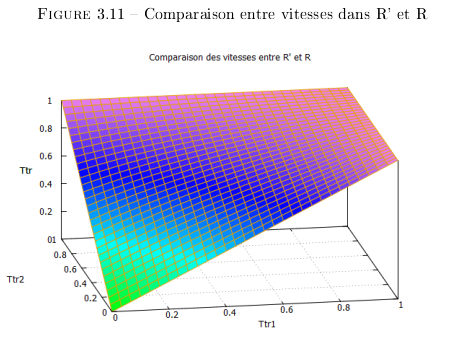
La comparaison des vitesses dans  et
et  donne la Figure 3.11
pour
donne la Figure 3.11
pour ![TTR1 appartient [0,1] TTR1 appartient [0,1]](images/EQ/TTR1-appartient-0-1.png) et
et ![TTR2 appartient [0,1] TTR2 appartient [0,1]](images/EQ/TTR2-appartient-0-1.png) .
Ce que nous montre ce modèle, c'est que dans le cas de
faibles vitesses entre
.
Ce que nous montre ce modèle, c'est que dans le cas de
faibles vitesses entre  et
et  , les vitesses dans
, les vitesses dans  observés dans
observés dans  sont
équivalentes. Par contre si la vitesse de
sont
équivalentes. Par contre si la vitesse de  s'approche de celle de
la lumière alors les vitesses observées, depuis
s'approche de celle de
la lumière alors les vitesses observées, depuis  (y
compris la vitesse de
(y
compris la vitesse de  par rapport à
par rapport à  ), tendent vers
), tendent vers 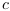 .
.
Par contre la projection de la vitesse 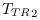 depuis le
repère
depuis le
repère  (en mouvement) dans le repère
(en mouvement) dans le repère  , fait apparaitre que plus
, fait apparaitre que plus
 est rapide par rapport à
est rapide par rapport à  , et plus la projection de la
vitesse (
, et plus la projection de la
vitesse (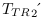 ) est petite. C'est ce que montrent la Figure
3.12 ainsi que l'équation, ci-avant, est
démontrée par l'EC.
8 (équation 3.14) en annexes.
) est petite. C'est ce que montrent la Figure
3.12 ainsi que l'équation, ci-avant, est
démontrée par l'EC.
8 (équation 3.14) en annexes.

Avec :
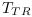 : Taux de transitions (
: Taux de transitions (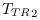 ) Observé
dans
) Observé
dans  ;
;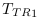 : Taux de transitions (vitesse) du référentiel
observé (vitesse de
: Taux de transitions (vitesse) du référentiel
observé (vitesse de  par rapport à
par rapport à  ) ;
) ;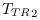 : Taux de transitions (vitesse) dans le
référentiel observé.
: Taux de transitions (vitesse) dans le
référentiel observé.
Transformation avec une repère en accélération uniforme
Jusqu'à présent nous avons effectué les comparaisons entre le modèle standard en se basant sur la juxtaposition de référentiels en mouvement uniforme l'un par rapport à l'autre. EC. 9 (en annexe montre la correspondance entre le modèle standard et le modèle CP.
Ce qui nous donne la correspondance entre la projection :
- Le modèle standard :
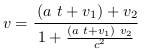 ;
; - Le modèle CP :
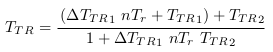 .
.
Avec :
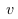 :
Transposition, dans le référentiel de
l'observateur (
:
Transposition, dans le référentiel de
l'observateur ( ),
de la vitesse Vitesse de l'objet après sont
accélération (dans le système standard) ;
),
de la vitesse Vitesse de l'objet après sont
accélération (dans le système standard) ;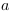 : Accélération de l'objet dans le
référentiel observé
: Accélération de l'objet dans le
référentiel observé  (dans le
système standard) ;
(dans le
système standard) ;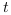 :
Durée de l'accélération de l'objet dans
le référentiel observé
:
Durée de l'accélération de l'objet dans
le référentiel observé  (dans le
système standard) ;
(dans le
système standard) ;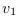 :
Vitesse initiale de l'objet dans le référentiel
observé
:
Vitesse initiale de l'objet dans le référentiel
observé  (dans le système standard) ;
(dans le système standard) ;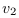 :
Vitesse du repère observé (
:
Vitesse du repère observé ( ) par rapport au
repère de l'observateur (
) par rapport au
repère de l'observateur ( ) (dans le système
standard) ;
) (dans le système
standard) ;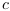 : La
vitesse de la lumière (dans le système standard)
;
: La
vitesse de la lumière (dans le système standard)
;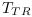 : Transposition, dans le
référentiel de l'observateur (
: Transposition, dans le
référentiel de l'observateur ( ), du taux de transition
de l'objet après application de la variation du taux de
transition (accélération) (dans le
système CP) ;
), du taux de transition
de l'objet après application de la variation du taux de
transition (accélération) (dans le
système CP) ;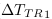 : Modification
(accélération) du taux de transition (vitesse)
de l'objet dans le référentiel
observé
: Modification
(accélération) du taux de transition (vitesse)
de l'objet dans le référentiel
observé  (dans le système CP) ;
(dans le système CP) ;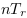 :
Nombre de transition durant lequel le taux de transitions
change (accélération) dans le
référentiel observé
:
Nombre de transition durant lequel le taux de transitions
change (accélération) dans le
référentiel observé  (dans le
système CP) ;
(dans le
système CP) ; 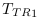 :
Taux de transitions (vitesse) initial de l'objet dans le
référentiel observé
:
Taux de transitions (vitesse) initial de l'objet dans le
référentiel observé  (dans le
système CP) ;
(dans le
système CP) ;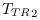 :
Taux de transitions (vitesse) du repère observé
(
:
Taux de transitions (vitesse) du repère observé
( )
par rapport au repère de l'observateur (
)
par rapport au repère de l'observateur ( ) dans le système
CP) ;
) dans le système
CP) ;
L'équation
est symétrique : 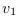 et et 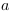 (système
standard) ou (système
standard) ou 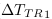 et et 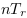 (système
CP) peuvent s'appliquer autant à l'objet dans (système
CP) peuvent s'appliquer autant à l'objet dans  qu'au mouvement de
qu'au mouvement de  par rapport à par rapport à  . .
|
En admettant que les vitesses entre les
référentiels est nulle (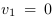 ou
ou 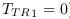 ) alors nous
ne prenons en considération que
l'accélération. En prenant
) alors nous
ne prenons en considération que
l'accélération. En prenant 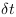 le plus faible
(
le plus faible
(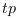 dans le système standard et 1 dans le système CP),
nous pouvons déterminer l'effet 'instantané' de
l'accélération de
dans le système standard et 1 dans le système CP),
nous pouvons déterminer l'effet 'instantané' de
l'accélération de  par rapport à
par rapport à  sur
les vitesses observées dans
sur
les vitesses observées dans  .
.
Les calculs sont plus simples dans le système CP
car 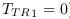 et
et 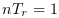 . Alors que dans le
système standard, il faut passer par
. Alors que dans le
système standard, il faut passer par 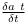 . Ceci venant de la discontinuité du
système CP par rapport à la continuité du
système standard.
. Ceci venant de la discontinuité du
système CP par rapport à la continuité du
système standard.
Nous en déduisons que :
- Le modèle CP est équivalent au modèle classique en mètres et secondes ;
- Dans le cas où l'accélération est nulle, nous nous retrouvons dans le cas classique de référentiel en mouvement uniforme ;
- Dans le cas où les référentiels
 et
et  sont immobiles l'un par rapport à l'autre en
sont immobiles l'un par rapport à l'autre en 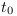 , alors les effets de
l'accélération sont équivalents aux
mouvements uniformes entre les repères ;
, alors les effets de
l'accélération sont équivalents aux
mouvements uniformes entre les repères ; - Du rapport entre
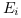 et
et 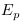 du modèle CP et que par
les conversions entre le modèle CP et le modèle
standard, nous retrouvons les résultats du
modèle standard ;
du modèle CP et que par
les conversions entre le modèle CP et le modèle
standard, nous retrouvons les résultats du
modèle standard ; - Dans le cas où l'accélération est
nulle, nous nous retrouvons dans le cas classique d'un
mouvement uniforme de
 par rapport à
par rapport à  ;
; - Dans le cas d'une vitesse nulle, les effets sont liés
à "l'accélération instantannée".La
définition de "l'accélération
instantanée" correspond à
l'accélération lorsque
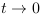 dans le modèle standard. Dans le modèle CP,
"l'accélération instantannée" correspond
à
dans le modèle standard. Dans le modèle CP,
"l'accélération instantannée" correspond
à 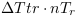 pour
pour 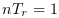 du fait de
la nature discrète du modèle CP. Les effets ne
peuvent être perçus (interaction) que lors d'une
transition de CP en CP. Ce qui implique que
du fait de
la nature discrète du modèle CP. Les effets ne
peuvent être perçus (interaction) que lors d'une
transition de CP en CP. Ce qui implique que 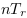 doit au minimum
être égale à 1. Ce qui se traduit (dans le
modèle standard) par
doit au minimum
être égale à 1. Ce qui se traduit (dans le
modèle standard) par 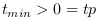 (temps de Planck). Ce qui est totalement inobservable aux
grandes échelles astronomiques.
(temps de Planck). Ce qui est totalement inobservable aux
grandes échelles astronomiques.
Table des matières :
- 1. Qu'est-ce qu'une Cellule de Planck (CP)
- 2. Propriétés des Cellules de Planck
- Harmonisation d'énergie, scission et fusion
- Scission et fusion
- Taux de transition et taux de création
- Unités de mesures et conversions entre modèle CP et Modèle standard
- 3. Compatibilité avec la relativité restreinte
- 4. La gravitation et l'expansion
- Corrélation entre système de mesures classique et système de mesure CP
- Principe de la déformation gravitationnelle
- Effet sur l'état de repos
- Mise en correspondance des référentiels locaux
- L'expansion une illusion ou une réalité ?
- La lumière : l'étalon universel ?
- Variation de l'énergie des CP
- Régime énergétique
- 5. Remerciements
- 6. Annexes
/!\ Attention ce document est classifié CONFIDENTIEL. Il ne peut être diffusé sans accord.

